Blog de Fisioterapia Fisioterapia
Artículos relacionados
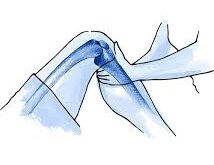
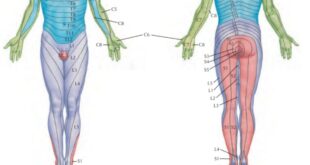
Esta prueba se utiliza para valorar una posible afectación de inestabilidad en rotación de la rodilla.
Posición del paciente: En decúbito supino, con los miembros superiores a lo largo del cuerpo y las rodillas extendidas.
Posición del fisioterapeuta: De pie, en el lado a valorar a la altura de las tibias en dirección craneal. Con la mano superior toma contacto sobre la región anterior de la rodilla a evaluar reposando el pulgar sobre el margen externo de la porción proximal del peroné.
Con la otra mano abarca el tercio distal de la tibia del mismo lado, de tal forma que contacte la pierna entre el flanco del abdomen y el antebrazo del fisioterapeuta.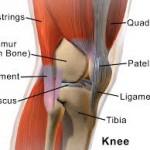
Ejecución del test: El fisioterapeuta induce con la ayuda de la mano inferior de forma pasiva un movimiento de rotación externa tibial y flexión de unos 40º de rodilla. Seguidamente, lleva a cabo un empuje de la rodilla hacia la línea media con la mano superior, induciendo tensión en valgo. A continuación conduce el miembro inferior hacia extensión de rodilla sin bloquear el movimiento de rotación tibial.
Interpretación del test: Si durante la maniobra se produce un movimiento de subluxación anterior de la rodilla por su porción externa acompañada o no de un chasquido, se puede pensar en una posible afectación del ligamento cruzado anterior. En este caso se dice que la prueba es positiva.
Es importante tener en cuenta la rotación externa tibial que el fisioterapeuta induce en el inicio de la prueba, ya que reduce un posible subluxación anterior. El resto de la maniobra ha de llevarse a cabo sin bloquear la rotación, pues debido a la rotación interna producida durante la flexión se induce un estrés del ligamento cruzado anterior.
